Steel4 Material

• Command_Manual
  • Tcl Commands
  • Modeling_Commands
    • model
    • uniaxialMaterial
    • ndMaterial
    • frictionModel
    • section
    • geometricTransf
    • element
    • node
    • sp commands
      • fix
      • fixX
      • fixY
      • fixZ
    • mp commands
      • equalDOF
      • rigidDiaphragm
      • rigidLink
    • timeSeries
    • pattern
    • mass
    • block commands
      • block2D
      • block3D
    • region
    • rayleigh
  • Analysis Commands
    • constraints Command
    • numberer Command
    • system Command
    • test Command
    • algorithm Command
    • integrator Command
    • analysis Command
    • eigen Command
    • analyze Command
  • Output Commands
    • recorder
    • record
    • print
    • printA
    • logFile
    • RealTime_Output_Commands
  • Misc Commands
    • eleResponse Command
    • getTime Command
    • getEleTags Command
    • getNodeTags
    • loadConst Command
    • nodeCoord Command
    • nodeDisp Command
    • nodeVel Command
    • nodeAccel Command
    • nodeEigenvector Command
    • nodeBounds
    • print Command
    • remove Command
    • reset Command
    • testIter
    • testNorms
    • wipe Command
    • exit Command
  • DataBase Commands
    • Template:DataBaseCommandsMenu

---

This command is used to construct a general uniaxial material with combined kinematic and isotropic hardening and optional non-symmetric behavior.

uniaxialMaterial Steel4 $matTag $f_y $E_0 < -asym > < -kin $b_k $R_0 $r_1 $r_2 < $b_kc $R_0c $r_1c $r_2c > > < -iso $b_i $rho_i $b_l $R_i $l_yp < $b_ic $rho_ic $b_lc $R_ic> > < -ult $f_u $R_u < $f_uc $R_uc > > < -init $sig_init > < -mem $cycNum >

Parameters

$matTag	unique material object integer tag
$f_y	yield strength (assumed identical in tension and compression)
$E_0	initial stiffness (Young's modulus)
optional features:

-kin	apply kinematic hardening

Kinematic hardening is based on the Menegotto-Pinto model. The parameters and their use is identical to those of the Steel02 material.
$b_k	hardening ratio (E_k/E_0)
$R_0	control the exponential transition from linear elastic to hardening asymptote recommended values: $R_0 = 20 $r_1 = 0.90 $r_2 = 0.15
$r_1
$r_2

-iso	apply isotropic hardening

Isotropic hardening increases the yield strength of the material. The applied increase is calculated as a function of the accumulated plastic strain. The following parameters control that function.
$b_i	initial hardening ratio (E_i/E_0)
$b_l	saturated hardening ratio (E_is/E_0)
$rho_i	specifies the position of the intersection point between initial and saturated hardening asymptotes
$R_i	control the exponential transition from initial to saturated asymptote
$l_yp	length of the yield plateau in eps_y0 = f_y / E_0 units

-ult	apply an ultimate strength limit

The ultimate strength limit serves as an upper limit of material resistance. After the limit is reached the material behaves in a perfectly plastic manner. Exponential transition is provided from the kinematic hardening to the perfectly plastic asymptote.
Note that isotropic hardening is also limited by the ultimate strength, but the transition from the isotropic hardening to the perfectly plastic asymptote is instantaneous.
$f_u	ultimate strength
$R_u	control the exponential transition from kinematic hardening to perfectly plastic asymptote

-asym

assume non-symmetric behavior

If non-symmetric behavior is assumed, material response under tension and compression will be controlled by two different parameter sets. The normal parameters control behavior under tension. Additional parameters shall be specified to describe behavior under compression. The following parameters are expected after the normal parameters when the options below are used.
-kin	$b_kc $R_0c $r_1c $r_2c
-iso	$b_ic $rho_ic $b_lc $R_ic
-ult	$f_uc $R_uc

-init

apply initial stress

Initial stress is assumed at 0 strain at the beginning of the loading process. The absolute value of the initial stress is assumed to be less than the yield strength of the material.
$sig_init	initial stress value

-mem	configure the load history memory

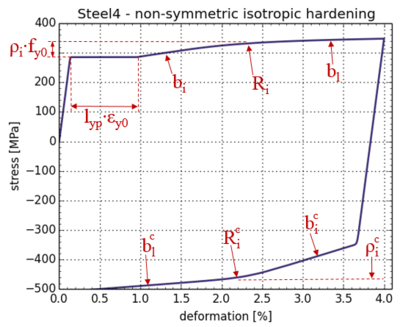
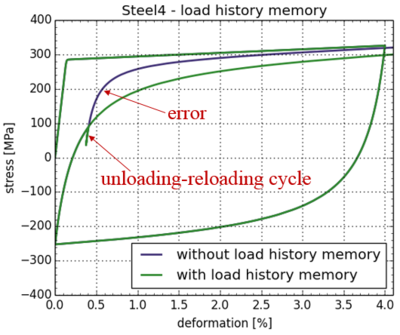
The load history memory is a database of preceding load cycles. It is updated at every load reversal point during the loading process. It is turned on by default. Turning it off will reduce the memory consumption of Steel4.
The available data on preceding cycles is currently used to correct a typical error in the Steel02 material. The error stems from the formulation of the Menegotto-Pinto kinematic hardening model. It leads to overestimation of the stress response after small unloading-reloading cycles. This phenomenon is important, because the seismic response of structures typically includes a large number of such small cycles. The error is avoided by forcing the kinematic hardening component of the response to converge to previous load cycles.
The load history memory can be used in the future to describe other characteristics of the response that depend on preceding load cycles.
$cycNum	expected number of half-cycles during the loading process
	Efficiency of the material can be slightly increased by correctly setting this value. The default value is $cycNum = 50
	Load history memory can be turned off by setting $cycNum = 0.

Examples

Coming soon...

Author:

Adam Zsarnóczay: zsarnoczay@vbt.bme.hu