CastFuse Material

• Command_Manual
  • Tcl Commands
  • Modeling_Commands
    • model
    • uniaxialMaterial
    • ndMaterial
    • frictionModel
    • section
    • geometricTransf
    • element
    • node
    • sp commands
      • fix
      • fixX
      • fixY
      • fixZ
    • mp commands
      • equalDOF
      • rigidDiaphragm
      • rigidLink
    • timeSeries
    • pattern
    • mass
    • block commands
      • block2D
      • block3D
    • region
    • rayleigh
  • Analysis Commands
    • constraints Command
    • numberer Command
    • system Command
    • test Command
    • algorithm Command
    • integrator Command
    • analysis Command
    • eigen Command
    • analyze Command
  • Output Commands
    • recorder
    • record
    • print
    • printA
    • logFile
    • RealTime_Output_Commands
  • Misc Commands
    • eleResponse Command
    • getTime Command
    • getEleTags Command
    • getNodeTags
    • loadConst Command
    • nodeCoord Command
    • nodeDisp Command
    • nodeVel Command
    • nodeAccel Command
    • nodeEigenvector Command
    • nodeBounds
    • print Command
    • remove Command
    • reset Command
    • testIter
    • testNorms
    • wipe Command
    • exit Command
  • DataBase Commands
    • Template:DataBaseCommandsMenu

---

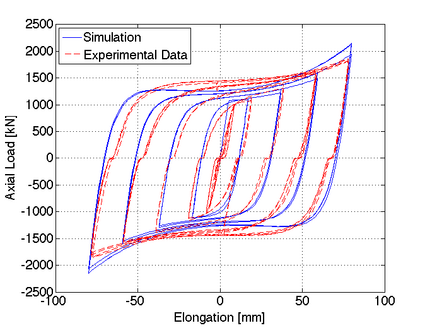
This command is used to construct a CastFuse uniaxial material. The CastFuse material simulates the hysteretic response a cast yielding fuse (CSF) for concentrically braced frames. The details of a CSF-brace are discussed in Gray et al. [1,2]. Isotropic hardening is modeled with the rules developed by Filippou et al. [3].

uniaxialMaterial Cast $matTag $n $bo $h $fy $E $L $b $Ro $cR1 $cR2 <$a1 $a2 $a3 $a4>

---

$matTag	integer tag identifying material
$n	Number of yield fingers of the CSF-brace
$bo	Width of an individual yielding finger at its base of the CSF-brace
$h	Thickness of an individual yielding finger
$fy	Yield strength of the steel material of the yielding finger
$E	Modulus of elasticity of the steel material of the yielding finger
$L	Height of an individual yielding finger
$b	Strain hardening ratio
$Ro	Parameter that controls the Bauschinger effect. Recommended Values for $Ro=between 10 to 30
$cR1	Parameter that controls the Bauschinger effect. Recommended Value $cR1=0.925
$cR2	Parameter that controls the Bauschinger effect. Recommended Value $cR2=0.150
$a1	isotropic hardening parameter, increase of compression yield envelope as proportion of yield strength after a plastic deformation of $a2*(Pp/Kp)
$a2	isotropic hardening parameter (see explanation under $a1). (optional default = 1.0)
$a3	isotropic hardening parameter, increase of tension yield envelope as proportion of yield strength after a plastic deformation of $a4*(Pp/Kp)
$a4	isotropic hardening parameter (see explanation under $a3). (optional default = 1.0)

---

Gray et al. [1] showed that the monotonic backbone curve of a CSF-brace with known properties (n, bo, h, L, fy, E) after yielding can be expressed as a close-form solution that is given by,

P = Pp/cos(2d/L), in which d is the axial deformation of the brace at increment i and Pp is the yield strength of the CSF-brace and is given by the following expression

Pp = nboh2fy/4L

The elastic stiffness of the CSF-brace is given by,

Kp = nboEh3fy/6L3

---

Examples:

1. Input parameters:

Assume a CSF-Brace with n=10 yielding fingers, bo=250mm, h = 34mm fy=0.365kN/mm2, E=200kN/mm2, L=250mm. These design parameters are the ones used by Gray et al. [1] in order to design a CSF-brace that was tested at the University of Toronto. This brace is used for calibration of the simulated hysteretic response of the CastFuse material implemented in Opensees. For this purpose, the following set of parameters are utilized:

uniaxialMaterial Cast 1 10 250.0 34.0 0.365 200.0 250.0 0.000 19.0 0.925 0.15 0.02 0.70 0.02 0.70

Using these properties a comparison between simulated and experimental response of a CSF brace tested at University of Toronto is shown in Figure 1.

Figure 1. CSF-Brace with n=10 yielding fingers, bo=250mm, h = 34mm fy=0.365kN/mm2, E=200kN/mm2, L=250mm, (Experimental data from Gray et al. [1])

---

References:

[1]	Gray, M.G., Christopoulos, C., Packer, J.A., (2010). "Cast Steel Yielding Fuse for Concentrically Braced Frames," Proceedings of the 9th U.S. National and 10th Canadian Conference on Earthquake Engineering, July 25-29, 2010, Toronto, Ontario, Canada, paper No. 595.
[2]	Gray, M.G., Christopoulos, C., Packer, J.A., Lignos, D.G. (2012). "Development, Validation and Modeling of the New Cast Steel Yielding Brace System,” Proceedings ASCE Structures Congress, March 29th-31st, Chicago, IL, USA, SEI institute.
[3]	Filippou, F. C., Popov, E. P., Bertero, V. V. (1983). "Effects of Bond Deterioration on Hysteretic Behavior of Reinforced Concrete Joints," Report EERC 83-19, Earthquake Engineering Research Center, University of California, Berkeley.

Code Developed by : by Dr. Dimitrios G. Lignos, (McGill University)