ConfinedConcrete01 Material

• Command_Manual
  • Tcl Commands
  • Modeling_Commands
    • model
    • uniaxialMaterial
    • ndMaterial
    • frictionModel
    • section
    • geometricTransf
    • element
    • node
    • sp commands
      • fix
      • fixX
      • fixY
      • fixZ
    • mp commands
      • equalDOF
      • rigidDiaphragm
      • rigidLink
    • timeSeries
    • pattern
    • mass
    • block commands
      • block2D
      • block3D
    • region
    • rayleigh
  • Analysis Commands
    • constraints Command
    • numberer Command
    • system Command
    • test Command
    • algorithm Command
    • integrator Command
    • analysis Command
    • eigen Command
    • analyze Command
  • Output Commands
    • recorder
    • record
    • print
    • printA
    • logFile
    • RealTime_Output_Commands
  • Misc Commands
    • eleResponse Command
    • getTime Command
    • getEleTags Command
    • getNodeTags
    • loadConst Command
    • nodeCoord Command
    • nodeDisp Command
    • nodeVel Command
    • nodeAccel Command
    • nodeEigenvector Command
    • nodeBounds
    • print Command
    • remove Command
    • reset Command
    • testIter
    • testNorms
    • wipe Command
    • exit Command
  • DataBase Commands
    • Template:DataBaseCommandsMenu

---

This 
command 
is 
used 
to 
construct 
an 
uniaxial
 material 
object 
of 
confined
 concrete 
in 
according 
to
 the
 work 
of 
Braga, 
Gigliotti
 and 
Laterza
 (2006). 
The
 confined
 concrete 
model
 (BGL
model) 
has 
not
 tensile
 strength 
and 
degraded
 linear 
unloading/reloading
 stiffness
 as 
proposed
 by 
Karsan 
and 
Jirsa
 (1969).
 The 
BGL 
model 
accounts 
for 
confinement
 effects 
due
 to 
different 
arrangements 
of 
transverse
 reinforcement 
and/or
 external 
strengthening
 such
 as 
steel 
jackets 
or 
FRP 
wraps. 
The 

confinement 
effect 
along
 the 
column is described 
as 
well.
 In
 order 
to 
obtain 
th e
compressive 
envelope 
curve a
 non
 linear 
approach 
is 
performed
 at 
each
 increment
 of 
column
 axial
 strain.
The
 sougth
 curve 
is 
obtained
 crossing 
different 
stress‐strain
 relationships,
 each 
of 
which
 corresponding
 to 
a 
different
 level 
of 
confinement.
 Currently,
 the
 Attard
 and
 Setunge’s
 model
 is
 implemented
 in
 calculating
 each
 active
 curve
 of
 the
 confined
 concrete.


uniaxialMaterial ConfinedConcrete01 $tag $secType $fpc $Ec (<-epscu $epscu> OR <-gamma $gamma>) (<-nu $nu> OR <-varub> OR <-varnoub>) $L1 ($L2) ($L3) $phis $S $fyh $Es0 $haRatio $mu $phiLon <-internal $phisi $Si $fyhi $Es0i $haRatioi $mui> <-wrap $cover $Am $Sw $fuil $Es0w> <-gravel> <-silica> <-tol $tol> <-maxNumIter $maxNumIter> <-epscuLimit $epscuLimit> <-stRatio $stRatio>

---

$tag	integer tag identifying material.
$secType	tag for the transverse reinforcement configuration. See NOTE 1.
$fpc	unconfined cylindrical strength of concrete specimen.
$Ec	initial elastic modulus of unconfined concrete.
<-epscu $epscu> OR <-gamma $gamma>	confined concrete ultimate strain. See NOTE 2.
<-nu $nu> OR <-varub> OR <-varnoub>	Poisson's Ratio. See NOTE 3.
$L1	length/diameter of square/circular core section measured respect to the hoop center line.
($L2), ($L3)	additional dimensions when multiple hoops are being used. See NOTE 4.
$phis	hoop diameter. If section arrangement has multiple hoops it refers to the external hoop.
$S	hoop spacing.
$fyh	yielding strength of the hoop steel.
$Es0	elastic modulus of the hoop steel.
$haRatio	hardening ratio of the hoop steel.
$mu	ductility factor of the hoop steel.
$phiLon	diameter of longitudinal bars.
<-internal $phisi $Si $fyhi $Es0i $haRatioi $mui>	optional parameters for defining the internal transverse reinforcement. If they are not specified they will be assumed equal to the external ones (for S2, S3, S4a, S4b and S5 typed).
<-wrap $cover $Am $Sw $ful $Es0w>	optional parameters required when section is strengthened with FRP wraps. See NOTE 5.

NOTES:

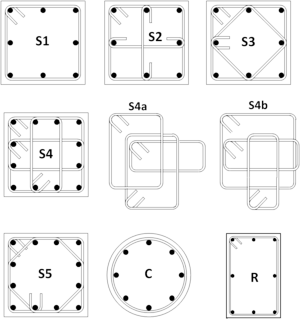
1) The following section types are available:

S1	square section with S1 type of transverse reinforcement with or without external FRP wrapping;
S2	square section with S2 type of transverse reinforcement with or without external FRP wrapping;
S3	square section with S3 type of transverse reinforcement with or without external FRP wrapping;
S4a	square section with S4a type of transverse reinforcement with or without external FRP wrapping;
S4b	square section with S4b type of transverse reinforcement with or without external FRP wrapping;
S5	square section with S5 type of transverse reinforcement with or without external FRP wrapping;
C	circular section with or without external FRP wrapping;
R	rectangular section with or without external FRP wrapping.

2) The confined concrete ultimate strain is defined using -epscu or -gamma. When -gamma option is specified, $gamma is the ratio of the strength corresponding to ultimate strain to the peak strength of the confined concrete stress-strain curve. If $gamma cannot be achieved in the range [0, $epscuLimit] then $epscuLimit (optional, default: 0.05) will be assumed as ultimate strain.

3) Poisson's Ratio is specified by one of these 3 methods: a) providing $nu using the -nu option. b) using the -varUB option in which Poisson’s ratio is defined as a function of axial strain by means of the expression proposed by Braga et al. (2006) with the upper bound equal to 0.5; or c) using the -varNoUB option in which case Poisson’s ratio is defined as a function of axial strain by means of the expression proposed by Braga et al. (2006) without any upper bound.

4) $L1 (2l), $L2 (a) and $L3 (b) are required when either S4a or S4b section types is used. $L1 (2d) and $L2 (2c) must be used for rectangular section.

5) When external stengthening is used must be specified the following parameters:

$cover	cover thickness measured from the outer line of hoop.
$Am	total area of FRP wraps.
$Sw	spacing of FRP wraps.
$ful	ultimate strength of FRP wraps.
$Es0w	elastic modulus of FRP wraps.

6) Stresses
 and
 strains
 can
 be
 defined
 either
 as
 positive
 or
 as
 negative
 values.
 All
 commands
 are 
not 
case 
sensitive.


EXAMPLES:

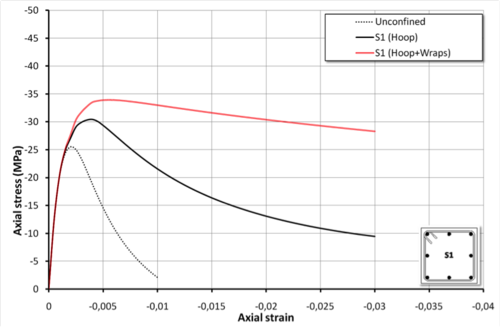
Square 
section 
reinforced 
by 
simple 
transverse 
hoop
 and
 by
 additional
 FRP
 wraps 
(Section
 S1)

Section S1

#uniaxialMaterial ConfinedConcrete01 $tag  $secType $fpc   $Ec    -epscu $epscu  $nu   $L1  $phis  $S   $fyh   $Es0   $haRatio  $mu   $phiLon  -stRatio  $stRatio
uniaxialMaterial ConfinedConcrete01    1     S1    -30.0  26081.0 -epscu -0.03 -varub 300.0 10.0 100.0 300.0 206000.0    0.0   1000.0   16.0   -stRatio    0.85

Section S1 strengthened by additional FRP wraps

#uniaxialMaterial ConfinedConcrete01 $tag  $secType $fpc   $Ec    -epscu $epscu  $nu   $L1  $phis   $S   $fyh   $Es0   $haRatio  $mu  phiLon      $cover $Am    $Sw  $ful    $Es0w    -stRatio  $stRatio
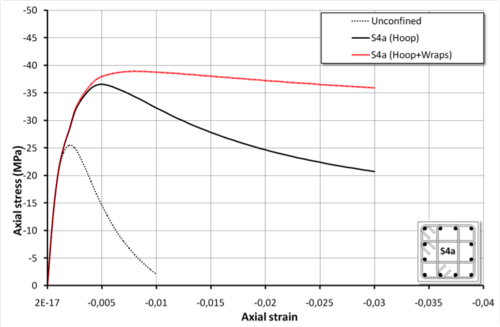
uniaxialMaterial ConfinedConcrete01   1      S1    -30.0  26081.0 -epscu -0.03 -varub 300.0  10.0  100.0 300.0 206000.0  0.0   1000.0  16.0 -wrap  30.0  51.0  100.0 3900.0 230000.0  -stRatio   0.85

Square 
section 
reinforced 
by 
multiple 
transverse 
hoop
 and
 by
 additional
 FRP
 wraps 
(Section
 S4a)

Section S4a

#uniaxialMaterial ConfinedConcrete01 $tag $secType $fpc  $Ec     -epscu $epscu $nu    $L1   $L2   $L3   $phis $S    $fyh  $Es0     $haRatio $mu    $phiLon -stRatio $stRatio
uniaxialMaterial ConfinedConcrete01  1    S4a      -30.0 26081.0 -epscu -0.03  -varUB 300.0 200.0 100.0 10.0  100.0 300.0 206000.0  0.0     1000.0 16.0    -stRatio  0.85

Section S4a strengthened by additional FRP wraps

#uniaxialMaterial ConfinedConcrete01 $tag $secType $fpc  $Ec     -epscu $epscu $nu    $L1   $L2   $L3   $phis $S    $fyh  $Es0     $haRatio $mu    $phiLon      $cover $Am  $Sw   $ful   $Es0w    -stRatio $stRatio
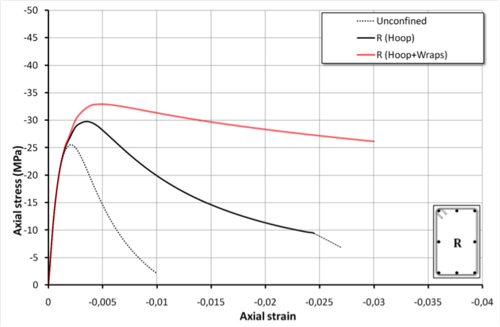
uniaxialMaterial ConfinedConcrete01  1    S4a      -30.0 26081.0 -epscu -0.03  -varUB 300.0 200.0 100.0 10.0  100.0 300.0 206000.0 0.0      1000.0 16.0   -wrap 30.0   51.0 100.0 3900.0 230000.0 -stRatio 0.85

Rectangular 
section 
reinforced 
by 
simple 
transverse 
hoop
 and
 by
 additional
 FRP
 wraps 
(Section
 R)

Section R

#uniaxialMaterial ConfinedConcrete01 $tag $secType $fpc  $Ec     -epscu $epscu $nu    $L1   $L2   $phis $S    $fyh  $Es0     $haRatio $mu    $phiLon -stRatio $stRatio
uniaxialMaterial ConfinedConcrete01  1    R        -30.0 26081.0 -epscu -0.03  -varUB 500.0 300.0 10.0  100.0 300.0 206000.0 0.0      1000.0 16.0    -stRatio 0.85

Section R strengthened by additional FRP wraps

#uniaxialMaterial ConfinedConcrete01 $tag $secType $fpc  $Ec     -epscu $epscu $nu    $L1   $L2   $phis $S    $fyh  $Es0     $haRatio $mu    $phiLon       $cover $Am  $Sw   $ful   $Es0w    -stRatio $stRatio
uniaxialMaterial ConfinedConcrete01  1    R        -30.0 26081.0 -epscu -0.03  -varUB 500.0 300.0 10.0  100.0 300.0 206000.0 0.0      1000.0 16.0    -wrap 30.0   51.0 100.0 3900.0 230000.0 -stRatio 0.85

---

REFEERENCES:

1. Attard, M. M., Setunge, S., 1996. “Stress-strain relationship of confined and unconfined concrete”. Material Journal ACI, 93(5), 432-444
2. Braga, F., Gigliotti, R., Laterza, M., 2006. “Analytical stress-strain relationship for concrete confined by steel stirrups and/or FRP jackets”. Journal of Structural Engineering ASCE, 132(9), 1402-1416.
3. D’Amato M., February 2009. “Analytical models for non linear analysis of RC structures: confined concrete and bond-slips of longitudinal bars”. Doctoral Thesis. University of Basilicata, Potenza, Italy.
4. Karsan, I. D., Jirsa, J. O., 1969. “Behavior of concrete under compressive loadings”, Journal of Structural Division ASCE, 95(12), 2543-2563.

---

Code Developed by: Michele D'Amato, University of Basilicata, Italy