Dynamic 2D Effective Stress Analysis of Slope

From OpenSeesWiki
Revision as of 22:50, 26 October 2010 by Mcganncr (talk | contribs)
Jump to navigation Jump to search

Example posted by: Christopher McGann, University of Washington

THIS PAGE IS UNDER CONSTRUCTION

This article describes the OpenSees implementation of an effective stress analysis of a slope which is subject to a seismic event. The slope is modeled in two-dimensions and it is assumed that the slope is underlain by an elastic half-space. The free-field response of the soil is considered through the use of massive columns of soil with periodic boundary conditions located at both ends of the model. Nine-node quadrilateral elements with both displacement and pore pressure degrees of freedom enable the model to track changes in pore pressure and effective stress during the course of the analysis. A Lysmer-Kuhlemeyer (1969) dashpot is utilized to account for the finite rigidity of the underlying elastic medium.

This article also discusses the use of the tool GiD as a means for post-process visualization of the results of the analysis. Files are provided which convert the recorded output from OpenSees into a format which can be read by GiD and the processes behind this are briefly discussed. The pre-processing capabilities of GiD, and the application of these capabilities to the generation of the input file for this example, are discussed in a separate example, GiD ProblemTypes for 2D Slope Analysis Input File Generation. The GiD tool can be downloaded from http://gid.cimne.upc.es/download.

Note: Some of the details of this analysis are shared with the Effective Stress Site Response Analysis of a Layered Soil Column example posted in the Practical Examples area of this manual. The user is referred to that example for further information on details which may be omitted or quickly explained here.


Provided with this article are several files. Files which are required for the analysis are indicated. The files include:

  • The example input file, slopeAnalysis2Deff.tcl (required for analysis)
  • The velocity time history of the selected earthquake record, velocityHistory.out (required for analysis)
  • A series of Matlab scripts (flaviaWriter.m, dispFlavia.m, porePressFlavia.m, ppRatioFlavia.m, stressFlavia.m) which can be used to reformat the recorded displacement, pore pressure, and stress data into a file which can be read by GiD for post-process visulization. Non-Matlab users may find the process represented by these files useful in creating an alternative means for accomplishing this reformatting.
  • A Matlab script, processMotion.m, which takes a particular acceleration time history, in this case the file GilroyNo1EW.out, and converts it into a velocity time history through numerical integration using the trapezoidal rule.

All of the files mentioned above can be downloaded by clicking here.


To run this example, the user must download the input file, slopeAnalysis2Deff.tcl, and the velocity time history file, velocityHistory.out, and place them in a single directory. Once this has been done, the user can then run the analysis. The additional files described above are not essential to the analysis. They are provided to demonstrate how to use the GiD tool to visualize results from this type of analysis.


Model Description

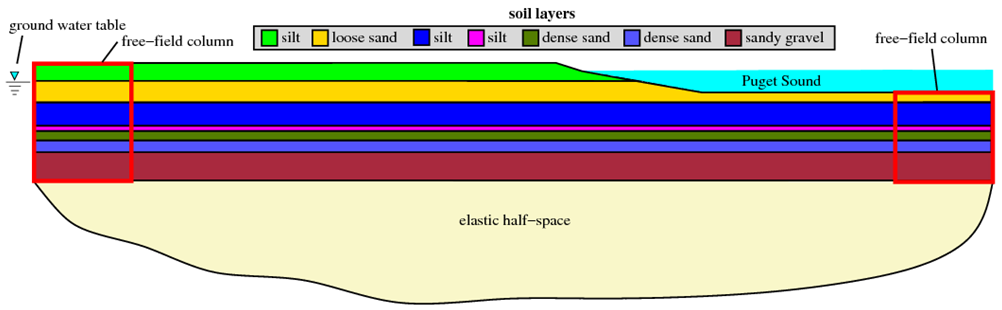
Fig. 1: Schematic of the slope site modeled in this example. The locations of the massive free-field columns are indicated.


The analysis discussed in this article is for the site shown in Fig. 1 above. There are several layers of cohesive and cohesionless material which make up this site, and the site is partially submerged below a body of water. The groundwater table in the portion of the site away from Puget Sound is assumed to have a constant elevation. The entire site is underlain by an elastic half-space, allowing some of the energy imparted by the seismic event to be removed from the site in a manner consistent with the existence of layer of bedrock below the slope site. The elastic half-space is modeled using a Lysmer-Kuhlemeyer (1969) dashpot in a similar manner to that used in the effective and total stress site response examples posted in the Practical Examples section of this manual.

Mesh Geometry

The input file for this example analysis, slopeAnalysis2Deff.tcl, was generated using the GiD problemtype UWnineQuad2Dup.gid, which is provided and discussed in a separate example, GiD ProblemTypes for 2D Slope Analysis Input File Generation. Using this problemtype, it is possible to create the mesh geometry visually in GiD, and export this information, along with additional conditions such as nodal fixities and material assignments, into an input file which can be read by OpenSees. Further details into this process can be found in the GiD ProblemTypes for 2D Slope Analysis Input File Generation example.

The mesh created for this example using GiD as a pre-processor is shown in Fig. 2. The use of the GiD tool greatly simplifies mesh-generation for 2D problems as compared to creating the nodes using loops inside the input file. The benefit is especially evident when mesh modifications or refinement are necessary.

Fig. 2: Mesh for slope analysis example. This mesh was generated using GiD.


The formulation of the nine-node quadrilateral elements used in this example necessitates care in the number of degrees of freedom which are currently in the domain when defining certain aspects of the model. The corner nodes of the elements must be created in a domain which considers three degrees of freedom, while the interior nodes of the elements must be created in a domain which considers only two degrees of freedom. This is also true of the fixities, masses, and loads applied to these two sets of nodes. Further discussion on the nine-node quadrilateral elements is available in the example, Effective Stress Site Response Analysis of a Layered Soil Column.

Boundary Conditions

The boundary conditions are assigned with the intention that the soil elements which model the slope and surrounding material are subject to the free-field ground motion. This is accomplished by using massive columns of soil elements on the two ends of the site. The displacement degrees of the freedom for the nodes on either side of these columns are tied together using equalDOF

When the horizontal excitation is applied to the model, these massive columns react to the motion independently of the attached site elements, hence the term free-field columns.

Retrieved from "https://opensees.ist.berkeley.edu/wiki/index.php?title=Dynamic_2D_Effective_Stress_Analysis_of_Slope&oldid=5897"