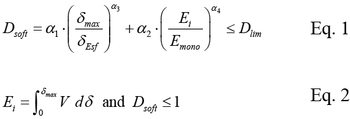RotationShearCurve

From OpenSeesWiki
Revision as of 19:42, 11 April 2014 by Ghannoum (talk | contribs)
Jump to navigation Jump to search




This command is used to construct a limit surface that defines the ultimate deformation between two nodes and/or the ultimate force that trigger lateral-strength degradation in the PinchingLimitStateMaterial. The curve can be used in two modes: 1) direct input mode, where all parameters are input; and 2) calibrated mode for shear-critical concrete columns, where only key column properties are input for model to fully define pinching and damage parameters. Note: when both strength and rotation limits are used. Lateral-strength degradation is triggered in the material model when the first limit is reached.


MODE 1: Direct Input

limitCurve RotationShearCurve $crvTag $eleTag $ndI $ndJ $rotAxis $Vn $Vr $Kdeg $rotLim
$crvTag unique limit curve object integer tag
$eleTag integer element tag to define the associated beam-column element used to extract axial load
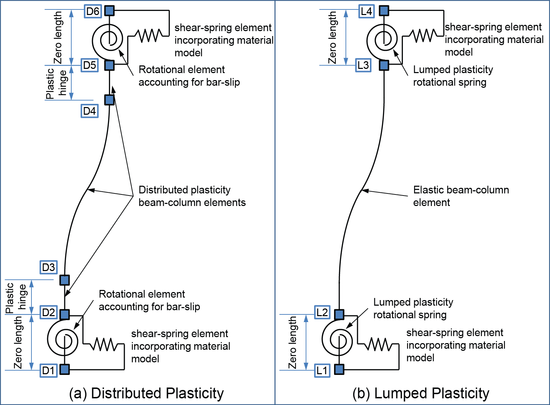
$ndI integer node tag to define the node at the extreme end of the frame member bounding the plastic hinge (L1 or D1 for bottom spring and L4 or D6 for top spring in Figure)
$ndJ integer node tag to define the node bounding the plastic hinge (L2 or D3 for bottom spring and L3 or D4 for top spring in Figure)
$rotAxis integer to indicate axis of measured rotation when triggering lateral-strength degradation
rotAxis = 3 – Rotation about z-axis – 2D

rotAxis = 4 – Rotation about x-axis – 3D

rotAxis = 5 – Rotation about y-axis – 3D

rotAxis = 6 – Rotation about z-axis – 3D

$Vn floating point value to define the ultimate strength in material model
Vn = -1 – strength limit is not used.

Vn > 0 – strength limit is the input value ]

$Vr floating point value to define the backbone residual strength
Vr = -1 – Residual strength = 0.2*(max. force in material model at initiation of degradation).

-1 < Vr < 0 – Residual shear strength = -Vr *( max. force in material model at initiation of degradation). Vr > 0 – Residual strength is the input value

$Kdeg floating point value to define the backbone degrading slope of the material model.
Note: the degrading slope must be less than zero.
$rotLim floating point value to limit the rotational capacity across the plastic hinge (difference between $ndI and $ndJ in absolute value). When this value (radians) is exceeded during the analysis degrading behavior is triggered in the material model.

MODE 2: Calibrated Model for Shear-Critical Concrete Columns

uniaxialMaterial PinchingLimitStateMaterial $matTag $nodeT $nodeB $driftAxis $Kelas $crvTyp $crvTag $eleTag $b $d $h $a $st $As $Acc $ld $db $rhot $f'c $fy $fyt
$matTag unique material object integer tag
$nodeT integer node tag to define the first node at the extreme end of the associated flexural frame member (L3 or D5 in Figure)
$nodeB integer node tag to define the last node at the extreme end of the associated flexural frame member (L2 or D2 in Figure)
$driftAxis integer to indicate the drift axis in which lateral-strength degradation will occur. This axis should be orthogonal to the axis of measured rotation (see $rotAxis in Rotation Shear Curve definition)

driftAxis = 1 – Drift along the x-axis driftAxis = 2 – Drift along the y-axis driftAxis = 3 – Drift along the z-axis

$Kelas floating point value to define the shear stiffness (Kelastic) of the shear spring prior to shear failure

Kelas = -4 – Shear stiffness calculated assuming double curvature and shear springs at both column element ends

Kelas = -3 – Shear stiffness calculated assuming double curvature and a shear spring at one column element end

Kelas = -2 – Shear stiffness calculated assuming single curvature and shear springs at both column element ends

Kelas = -1 – Shear stiffness calculated assuming single curvature and a shear spring at one column element end

Kelas > 0 – Shear stiffness is the input value

Note: integer inputs allow the model to know whether column height equals the shear span (cantelever) or twice the shear span (double curvature). For columns in frames, input the value for the case that best approximates column end conditions or manually input shear stiffness (typically double curvature better estimates framed column behavior)

$crvTag integer tag for the unique limit curve object associated with this material
$eleTag integer element tag to define the associated beam-column element used to extract axial load
$b floating point column width (inches)
$d floating point column depth (inches)
$h floating point column height (inches)
$a floating point shear span length (inches)
$st floating point transverse reinforcement spacing (inches) along column height
$As floating point total area (inches squared) of longitudinal steel bars in section
$Acc floating point gross confined concrete area (inches squared) bounded by the transverse reinforcement in column section
$ld floating point development length (inches) of longitudinal bars using ACI 318-11 Eq. 12-1 and Eq. 12-2
$db floating point diameter (inches) of longitudinal bars in column section
$rhot floating point transverse reinforcement ratio (Ast/st.db)
$f'c floating point concrete compressive strength (ksi)
$fy floating point longitudinal steel yield strength (ksi)
$fyt floating point transverse steel yield strength (ksi)

DESCRIPTION:


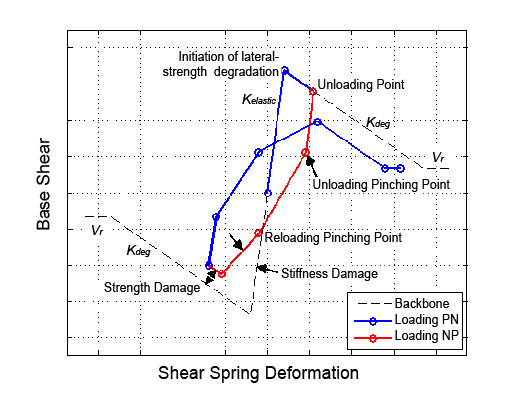
The material model coupled with the RotationShearCurve limit surface: 1) has the ability to continually monitor forces and deformations in the flexural elements for conditions that trigger lateral-strength degradation, 2) has a built-in function that compensates for flexural deformation offsets that arise from the degrading behavior of the material in shear springs, and 3) is able to trigger lateral-strength degradation through either a limiting lateral force or element deformations (whichever is reached first). The material introduces several functionalities that give users a high degree of control over the triggering of strength degradation and the ensuing cyclic degrading behavior. Damage algorithms are implemented to control the degrading behavior through elastic stiffness, reloading stiffness, and backbone strength degradation (Fig. 2). The rate of damage accumulation can be controlled by energy-, displacement-, and cycle-based damage computation algorithms.

During the degrading behavior, the model automatically adjusts reloading stiffness to achieve a symmetric global-element lateral load-vs lateral displacement behavior. The model does so by automatically adjusting the reloading stiffness and backbone curve of the material model to compensate for dissymmetry introduced by the unloading of the flexural elements in series with shear springs governed by the model.


DAMAGE:

Damage accumulations effects based on numbers of cycles can be introduced to reloading stiffness and backbone strength through the simple parameters $dmgRCyc and $dmgSCyc with values ranging from 0 to 1.

Elastic stiffness, reloading stiffness, and strength can be adjusted using the following energy and displacement damage model (from Mitra and Lowes (2007)):


EXAMPLE:

PinchingLimitStateMaterial Example


REFERENCES:

1. LeBorgne M. R., 2012, "Modeling the Post Shear Failure Behavior of Reinforced Concrete Columns." Austin, Texas: University of Texas at Austin, PhD, 301.

2. LeBorgne M. R. , Ghannoum W. M., 2013, "Analytical Element for Simulating Lateral-Strength Degradation in Reinforced Concrete Columns and Other Frame Members," Journal of Structural Engineering, V. doi: 10.1061/(ASCE)ST.1943-541X.0000925

3. Ghannoum W. M., Moehle J. P., 2012, "Rotation-Based Shear Failure Model for Lightly Confined Reinforced Concrete Columns," Journal of Structural Engineering, V. 138, No. 10, 1267-78.

4. Mitra Nilanjan, Lowes Laura N., 2007, "Evaluation, Calibration, and Verification of a Reinforced Concrete Beam--Column Joint Model," Journal of Structural Engineering, V. 133, No. 1, 105-20.

Retrieved from "https://opensees.ist.berkeley.edu/wiki/index.php?title=RotationShearCurve&oldid=11156"