UVCuniaxial (Updated Voce-Chaboche)

• Command_Manual
  • Tcl Commands
  • Modeling_Commands
    • model
    • uniaxialMaterial
    • ndMaterial
    • frictionModel
    • section
    • geometricTransf
    • element
    • node
    • sp commands
      • fix
      • fixX
      • fixY
      • fixZ
    • mp commands
      • equalDOF
      • rigidDiaphragm
      • rigidLink
    • timeSeries
    • pattern
    • mass
    • block commands
      • block2D
      • block3D
    • region
    • rayleigh
  • Analysis Commands
    • constraints Command
    • numberer Command
    • system Command
    • test Command
    • algorithm Command
    • integrator Command
    • analysis Command
    • eigen Command
    • analyze Command
  • Output Commands
    • recorder
    • record
    • print
    • printA
    • logFile
    • RealTime_Output_Commands
  • Misc Commands
    • eleResponse Command
    • getTime Command
    • getEleTags Command
    • getNodeTags
    • loadConst Command
    • nodeCoord Command
    • nodeDisp Command
    • nodeVel Command
    • nodeAccel Command
    • nodeEigenvector Command
    • nodeBounds
    • print Command
    • remove Command
    • reset Command
    • testIter
    • testNorms
    • wipe Command
    • exit Command
  • DataBase Commands
    • Template:DataBaseCommandsMenu

---

This command is used to construct an Updated Voce-Chaboche (UVC) material for uniaxial stress states. This material is a refined version of the classic nonlinear isotropic/kinematic hardening material model based on the Voce isotropic hardening law and the Chaboche kinematic hardening law. The UVC model contains an updated isotropic hardening law, with parameter constraints, to simulate the permanent decrease in yield stress with initial plastic loading associated with the discontinuous yielding phenomenon in mild steels. Details regarding the model, and implementation, can be found in the cited references at the end.

uniaxialMaterial UVCuniaxial $matTag $E $fy $QInf $b $DInf $a $N $C1 $gamma1 <$C2 $gamma2 $C3 $gamma3 … $C8 $gamma8>

---

$matTag	Integer tag identifying the material.
$E	Elastic modulus of the steel material.
$fy	Initial yield stress of the steel material.
$QInf	Maximum increase in yield stress due to cyclic hardening (isotropic hardening).
$b	Isotropic hardening saturation rate, b > 0.
$DInf	Difference between initial and steady-state yield stresses, to neglect the model updates set DInf = 0.
$a	Saturation rate of yield stress difference, a > 0. If DInf == 0, then a is arbitrary (but still a > 0).
$N	Number of backstresses to define, N >= 1.
$C1	Kinematic hardening parameter associated with backstress component 1.
$gamma1	Saturation rate of kinematic hardening associated with backstress component 1.
<$C2 $gamma2 $C3 $gamma3 … $C8 $gamma8>	Additional backstress parameters, up to 8 may be specified. If C is specified, then the corresponding gamma must also be specified. Note that only the first N backstresses will be read by the parser.

---

Examples

1. Validation:

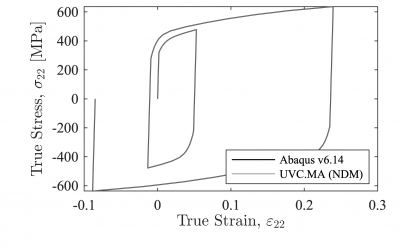
This first example compares the response of the UVC model with the built-in nonlinear isotropic/kinematic material model in Abaqus. For this validation the model updates are neglected by simply setting DInf = 0.0 and a = 1.0. The model parameters are:

E = 179800 MPa, fy = 318.5 MPa, QInf = 100.7 MPa, b = 8.0, DInf = 0.0 MPa, a = 1.0, C1 = 11608.2 MPa, gamma1 = 145.2, C2 = 1026.3 MPa, gamma2 = 4.7

Figure 1 shows that the two implementations agree to the level of machine precision. The models used to generate the Abaqus and OpenSees responses can be found at https://github.com/ahartloper/UVC_MatMod.

Figure 1. Validation of UVC model with built-in nonlinear isotropic/kinematic material in Abaqus.

2. Structural steels:

To be added.

---

Parameters for structural steels

Below is a list of model parameters for 12 structural steels.

UVC Material Parameters
Material	E	fy	QInf	b	DInf	a	C1	gamma1	C2	gamma2
-	[GPa]	[MPa]	[MPa]	-	[MPa]	-	[MPa]	-	[MPa]	-
S355J2+N (50 mm)	197.31	338.80	134.32	14.71	133.75	229.25	26242.00	199.04	2445.30	11.66
S355J2+N (25 mm)	185.97	332.18	120.48	8.14	93.15	261.75	21102.00	173.60	2300.60	10.42
S460NL (25 mm)	187.61	439.20	97.35	14.02	136.64	226.40	26691.00	188.75	2892.40	10.44
S690QL (25 mm)	188.63	685.39	0.11	0.11	132.30	285.15	34575.00	185.16	3154.20	20.14
A992 Gr. 50 (W14X82 web)	210.74	378.83	122.63	19.74	143.49	248.14	31638.00	277.32	1548.60	9.04
A992 Gr. 50 (W14X82 flange)	191.02	373.72	141.47	15.20	135.95	211.16	25621.00	235.12	942.18	3.16
A500 Gr. B (HSS305X16)	191.21	324.09	228.02	0.11	50.41	270.40	17707.00	207.18	1526.20	6.22
BCP325 (22 mm)	178.61	368.03	112.25	10.78	105.95	221.92	20104.00	200.43	2203.00	11.76
BCR295(HSS350X22)	178.74	412.21	0.09	0.09	103.30	212.83	20750.59	225.26	1245.04	2.09
HYP400(27mm)	189.36	454.46	62.63	16.57	109.28	145.74	13860.00	141.61	1031.10	3.53

---

References:

[1]	Hartloper, A. R., de Castro e Sousa A., and Lignos D.G. (2019). "Sensitivity of Simulated Steel Column Instabilities to Plasticity Model Assumptions". 12th Canadian Conference on Earthquake Engineering, Quebec City, QC, Canada.
[2]	Hartloper, A. R., de Castro e Sousa A., and Lignos D.G. (2019). "A Nonlinear Isotropic/Kinematic Hardening Model for Materials with Discontinuous Yielding". Report No. 271062, Resilient Steel Structures Laboratory (RESSLab), EPFL, Lausanne, Switzerland.