ViscousDamper Material

• Command_Manual
  • Tcl Commands
  • Modeling_Commands
    • model
    • uniaxialMaterial
    • ndMaterial
    • frictionModel
    • section
    • geometricTransf
    • element
    • node
    • sp commands
      • fix
      • fixX
      • fixY
      • fixZ
    • mp commands
      • equalDOF
      • rigidDiaphragm
      • rigidLink
    • timeSeries
    • pattern
    • mass
    • block commands
      • block2D
      • block3D
    • region
    • rayleigh
  • Analysis Commands
    • constraints Command
    • numberer Command
    • system Command
    • test Command
    • algorithm Command
    • integrator Command
    • analysis Command
    • eigen Command
    • analyze Command
  • Output Commands
    • recorder
    • record
    • print
    • printA
    • logFile
    • RealTime_Output_Commands
  • Misc Commands
    • eleResponse Command
    • getTime Command
    • getEleTags Command
    • getNodeTags
    • loadConst Command
    • nodeCoord Command
    • nodeDisp Command
    • nodeVel Command
    • nodeAccel Command
    • nodeEigenvector Command
    • nodeBounds
    • print Command
    • remove Command
    • reset Command
    • testIter
    • testNorms
    • wipe Command
    • exit Command
  • DataBase Commands
    • Template:DataBaseCommandsMenu

---

This command is used to construct a ViscousDamper material, which represents the Maxwell Model (linear spring and nonlinear dashpot in series). The ViscousDamper material simulates the hysteretic response of nonlinear viscous dampers. An adaptive iterative algorithm has been implemented and validated to solve numerically the constitutive equations within a nonlinear viscous damper with a high-precision accuracy.

uniaxialMaterial ViscousDamper $matTag $K $Cd $alpha <$LGap> < $NM $RelTol $AbsTol $MaxHalf>

---

$matTag	integer tag identifying material
$K	Elastic stiffness of linear spring (to model the axial flexibility of a viscous damper (brace and damper portion)
$Cd	Viscous parameter of damper
$alpha	Viscous damper exponent
$LGap	gap length to simulate the gap length due to the pin tolerance
$NM	Employed adaptive numerical algorithm (default value NM = 1; 1 = Dormand-Prince54, 2=6th order Adams-Bashforth-Moulton, 3=modified Rosenbrock Triple)
$RelTol	Tolerance for absolute relative error control of the adaptive iterative algorithm (default value 10^-6)
$AbsTol	Tolerance for absolute error control of adaptive iterative algorithm (default value 10^-10)
$MaxHalf	Maximum number of sub-step iterations within an integration step (default value 15)

---

Examples:

1. Input parameters:

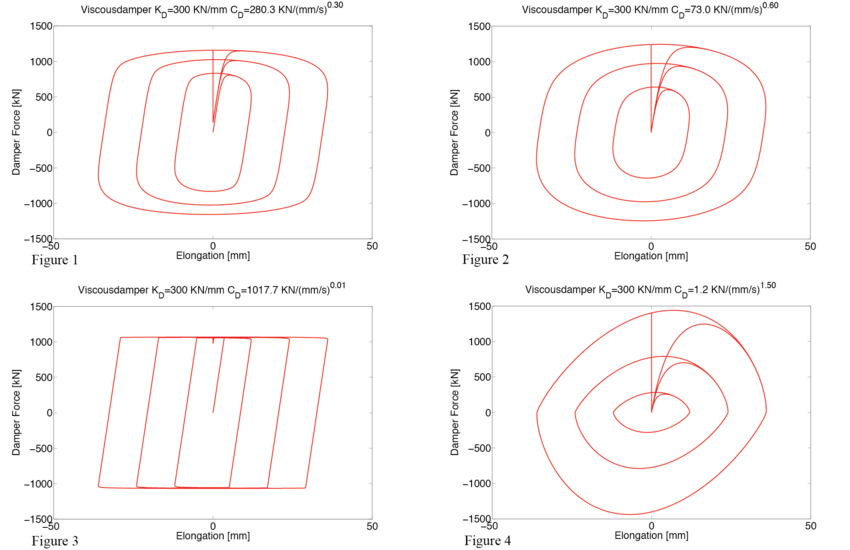
Assume a viscous damper with axial stiffness K=300.0kN/mm, viscous parameter Cd=280.3kN(s/mm)0.3, and exponent a=0.30.

The input parameters for the material should be as follows:

uniaxialMaterial ViscousDamper 1 300 280.3 0.30

Using these properties, Figure 1 shows the hysteretic response of this damper for sinusoidal displacement increments of 12, 24 and 36mm and a frequency f = 0.5Hz.

The sensitivity of the viscous damper with respect to its axial stiffness is shown in Figures 2 to 4 for the following set of parameters:

Viscous Damper with various input parameter variations

2. Single story single bay frame with viscous damper

---

References:

[1]	Akcelyan, S., Lignos, D. G., Hikino, T., and Nakashima, M. (2016). “Evaluation of simplified and state-of-the-art analysis procedures for steel frame buildings equipped with supplemental damping devices based on E-Defense full-scale shake table tests.” Journal of Structural Engineering, 142(6), 04016024. [1]
[2]	Oohara, K., and Kasai, K. (2002), “Time-History Analysis Models for Nonlinear Viscous Dampers”, Proc. Structural Engineers World Congress (SEWC), Yokohama, JAPAN, CD-ROM, T2-2-b-3 (in Japanese).
[3]	Kasai K, Oohara K. “Algorithm and Computer Code To Simulate Response of Nonlinear Viscous Damper” Passively Controlled Structure Symposium 2001, Yokohama, Japan (in Japanese).

Code Developed and Implemented by : Sarven Akcelyan & Prof. Dimitrios G. Lignos, (McGill University)