Pinching4 Material: Difference between revisions
(Created page with '{{CommandManualMenu}} This command is used to construct a uniaxial material that represents a 'pinched' load-deformation response and exhibits degradation under cyclic loading. ...') |
No edit summary |
||
| Line 53: | Line 53: | ||
NOTES: | NOTES: | ||
[[Image:Piinching4.jpg]] | |||
Damage Models: | |||
Stiffness and strength are assumed to deteriorate due to the imposed "load" history. The same basic equations are used to describe deterioration in strength, unloading stiffness and reloading stiffness: | |||
:<math>k_i = k_0(1 -\delta k_i)</math> | |||
where <math>k_i</math> is the unloading stiffness at time <math>t_i</math>, <math>k_0</math> is the initial unloading stiffness (for the case of no damage), and <math>\delta k_i</math>(defined below) is the value of the stiffness damage index at time <math>t_i</math>. | |||
:<math>d_{\text{max i}} = d_{\text{max 0}}(1 -\delta d_i)</math> | |||
where <math>d_{\text{max i}}</math> is the deformation demand that defines the end of the reload cycle for increasing deformation demand, <math>d_{\text{max 0}} </math> is the maximum historic deformation demand (which would be the deformation demand defining the end of the reload cycle if degradation of reloading stiffness is ignored), and <math>\delta d_i</math> (defined below) is the value of reloading stiffness damage index at time <math>t_i</math>. | |||
:<math>f_{\text{max i}} = f_{\text{max 0}}(1 -\delta f_i)</math> | |||
where <math>f_{\text{max i}}</math> is the current envelope maximum strength at time <math>t_i</math>, <math>f_{\text{max 0}} </math> is the initial envelope maximum strength for the case of no damage, and <math>\delta f_i</math> (defined below) is the value of strength value index at time <math>t_i</math>. | |||
The damage indices <math>\delta k_i</math>, <math>\delta d_i</math>, and <math>\delta f_i</math>, may be defined to be a function of displacement history only ($dmgType = "cycle") or displacement history and energy accumulation ($dmgType = "energy"). For either case, all of the damage indices are computed using the same basic equation. | |||
If the damage indices are assumed to be a function of displacement history and energy accumulation, the unloading stiffness damage index, <math>\delta k_i</math> is computed as follows: | |||
Revision as of 04:03, 24 March 2010
- Command_Manual
- Tcl Commands
- Modeling_Commands
- model
- uniaxialMaterial
- ndMaterial
- frictionModel
- section
- geometricTransf
- element
- node
- sp commands
- mp commands
- timeSeries
- pattern
- mass
- block commands
- region
- rayleigh
- Analysis Commands
- Output Commands
- Misc Commands
- DataBase Commands
This command is used to construct a uniaxial material that represents a 'pinched' load-deformation response and exhibits degradation under cyclic loading. Cyclic degradation of strength and stiffness occurs in three ways: unloading stiffness degradation, reloading stiffness degradation, strength degradation.
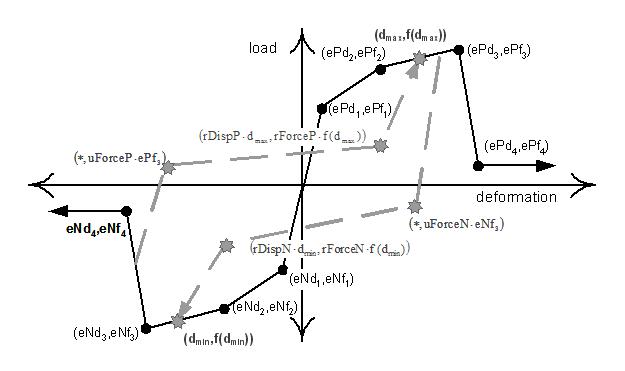
| uniaxialMaterial Pinching4 $matTag $ePf1 $ePd1 $ePf2 $ePd2 $ePf3 $ePd3 $ePf4 $ePd4 <$eNf1 $eNd1 $eNf2 $eNd2 $eNf3 $eNd3 $eNf4 $eNd4> $rDispP $rForceP $uForceP <$rDispN $rForceN $uForceN > $gK1 $gK2 $gK3 $gK4 $gKLim $gD1 $gD2 $gD3 $gD4 $gDLim $gF1 $gF2 $gF3 $gF4 $gFLim $gE $dmgType |
| $matTag | integer tag identifying material |
| $ePf1 $ePf2 $ePf3 $ePf4 | floating point values defining force points on the positive response envelope |
| $ePd1 $ePd2 $ePd3 $ePd4 | floating point values defining deformation points on the positive response envelope |
| $eNf1 $eNf2 $eNf3 $eNf4 | floating point values defining force points on the negative response envelope |
| $eNd1 $eNd2 $eNd3 $eNd4 | floating point values defining deformation points on the negative response envelope |
| $rDispP | floating point value defining the ratio of the deformation at which reloading occurs to the maximum historic deformation demand |
| $fFoceP | floating point value defining the ratio of the force at which reloading begins to force corresponding to the maximum historic deformation demand |
| $uForceP | floating point value defining the ratio of strength developed upon unloading from negative load to the maximum strength developed under monotonic loading |
| $rDispN | floating point value defining the ratio of the deformation at which reloading occurs to the minimum historic deformation demand |
| $fFoceN | floating point value defining the ratio of the force at which reloading begins to force corresponding to the minimum historic deformation demand |
| $uForceN | floating point value defining the ratio of strength developed upon unloading from negative load to the minimum strength developed under monotonic loading |
| $gK1 $gK2 $gK3 $gK4 $gKLim | floating point values controlling cyclic degradation model for unloading stiffness degradation |
| $gD1 $gD2 $gD3 $gD4 $gDLim | floating point values controlling cyclic degradation model for reloading stiffness degradation |
| $gF1 $gF2 $gF3 $gF4 $gFLim | floating point values controlling cyclic degradation model for strength degradation |
| $gE | floating point value used to define maximum energy dissipation under cyclic loading. Total energy dissipation capacity is defined as this factor multiplied by the energy dissipated under monotonic loading. |
| $dmgType | string to indicate type of damage (option: "cycle", "energy") |
| $beta | power used to determine the degraded unloading stiffness based on ductility, m-b (optional, default=0.0) |
| $curveTag | an integer tag for the LimitCurve defining the limit surface |
| $curveType | an integer defining the type of LimitCurve (0 = no curve,
1 = axial curve, all other curves can be any other integer) |
NOTES:
Damage Models:
Stiffness and strength are assumed to deteriorate due to the imposed "load" history. The same basic equations are used to describe deterioration in strength, unloading stiffness and reloading stiffness:
- <math>k_i = k_0(1 -\delta k_i)</math>
where <math>k_i</math> is the unloading stiffness at time <math>t_i</math>, <math>k_0</math> is the initial unloading stiffness (for the case of no damage), and <math>\delta k_i</math>(defined below) is the value of the stiffness damage index at time <math>t_i</math>.
- <math>d_{\text{max i}} = d_{\text{max 0}}(1 -\delta d_i)</math>
where <math>d_{\text{max i}}</math> is the deformation demand that defines the end of the reload cycle for increasing deformation demand, <math>d_{\text{max 0}} </math> is the maximum historic deformation demand (which would be the deformation demand defining the end of the reload cycle if degradation of reloading stiffness is ignored), and <math>\delta d_i</math> (defined below) is the value of reloading stiffness damage index at time <math>t_i</math>.
- <math>f_{\text{max i}} = f_{\text{max 0}}(1 -\delta f_i)</math>
where <math>f_{\text{max i}}</math> is the current envelope maximum strength at time <math>t_i</math>, <math>f_{\text{max 0}} </math> is the initial envelope maximum strength for the case of no damage, and <math>\delta f_i</math> (defined below) is the value of strength value index at time <math>t_i</math>.
The damage indices <math>\delta k_i</math>, <math>\delta d_i</math>, and <math>\delta f_i</math>, may be defined to be a function of displacement history only ($dmgType = "cycle") or displacement history and energy accumulation ($dmgType = "energy"). For either case, all of the damage indices are computed using the same basic equation.
If the damage indices are assumed to be a function of displacement history and energy accumulation, the unloading stiffness damage index, <math>\delta k_i</math> is computed as follows:
EXAMPLE:
DESCRIPTION:
Stiffness and strength are assumed to deteriorate due to the imposed "load" history. The same basic equations are used to describe deterioration in strength, unloading stiffness and reloading stiffness:
REFERENCES:
Code Developed by: Nilinjan Mitra, University of Washington