Impact Material
This command is used to construct an impact material object
| uniaxialMaterial ImpactMaterial $matTag $K1 $K2 $δy $gap
|
| $matTag | integer tag identifying material |
| $K1 | initial stiffness |
| $K2 | secondary stiffness |
| $δy | yield displacement |
| $gap | initial gap* |
NOTES:
This material is implemented as a compression-only gap material. Delta_y and gap should be input as negative values.
DESCRIPTION:
This material is based on an approximation to the Hertz contact model proposed by Muthukumar (See REFERENCES below). The energy dissipated during impact is:
E = kh * δm^(n+1) * (1-e^2) / (N+1)
where kh is the impact stiffness parameter, with a typical value of EA/L or 25,000 k-in.-3/2; n is typically taken as 3/2 for the exponent associated with the Hertz power rule; e is the coefficient of restitution, with typical values from 0.6-0.8; and δm is the maximum penetration during the pounding event. The effective stiffness, Keff, is:
Keff = kh * sqrt(δm)
The yield displacement is:
δy = a * δm
where a is typically taken as 0.1. The initial stiffness, K1, and secondary stiffness, K2, are then selected such that the Impact model dissipates an amount of energy during a pounding event that is consistent with the associated energy dissipated in the Hertz model.
K1 = Keff + E / (a*δm^2)
K2 = Keff - E / ((1-a)*δm^2)
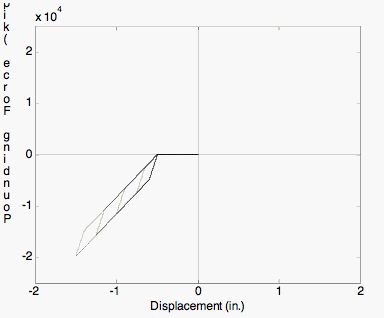
Response of Impact Material during a pounding event.
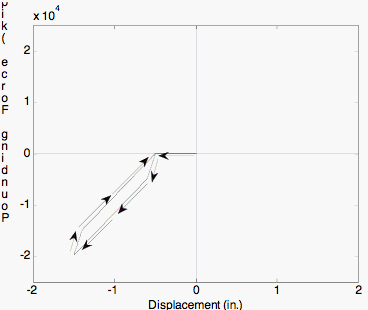
Response of Impact Material for displacement cycles of increasing amplitude.
EXAMPLE:
REFERENCES:
Muthukumar, S., and DesRoches, R. (2006). “A Hertz Contact Model with Non-linear Damping for Pounding Simulation.” Earthquake Engineering and Structural Dynamics, 35, 811-828.
Muthukumar, S. (2003). “A Contact Element Approach with Hysteresis Damping for the Analysis and Design of Pounding in Bridges.” PhD Thesis, Georgia Institute of Technology. http://smartech.gatech.edu/
Nielson, B. (2005). “Analytical Fragility Curves for Highway Bridges in Moderate Seismic Zones.” PhD Thesis, Georgia Institute of Technology. http://smartech.gatech.edu/
Code Developed by: Mathew Dryden, UC Berkeley